2_[datastructure]힙
힙 Heap
- 데이터에서 최댓값과 최솟값을 빠르게 찾기 위해 고안된 완전 이진 트리(Complete Binary Tree)
- 완전 이진 트리 : 노드를 삽입할 때 최하단 왼쪽 노드부터 차례대로 삽입하는 트리
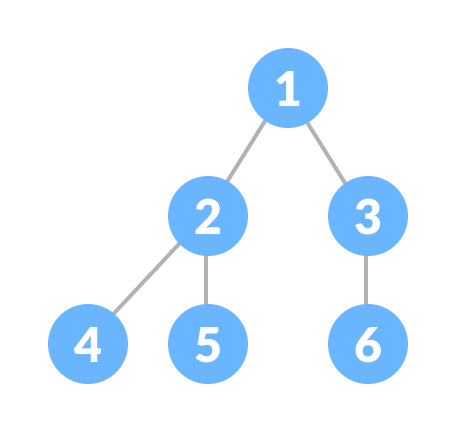
source: https://www.programiz.com/dsa/complete-binary-tree
- 힙을 사용하는 이유
- 배열을 사용해서 최댓값과 최솟값을 찾으면 O(n)의 시간이 소요됨 -힙에 데이터를 넣고 최댓값과 최솟값을 넣으면 O(logn)의 시간이 소요됨
- 우선순위 큐와 같이 최댓값 혹은 최솟값을 빠르게 찾아야 하는 자료구조 및 알고리즘 구현에 활용됨
- 힙 구조는 최댓값을 구하기 위한 구조(최대 힙 ; Max Heap)과 최솟값을 구하기 위한 구조(최소 힙; Min Heap)으로 분류될 수 있음
- 힙이 되기 위한 요건
- 최대 힙의 경우, 각 노드의 값 ≥ 해당 노드의 자식노드가 가진 값
- 최소 힙의 경우, 각 노드의 값 ≤ 해당 노드의 자식노드가 가진 값
- 완전 이진 트리 형태를 가짐
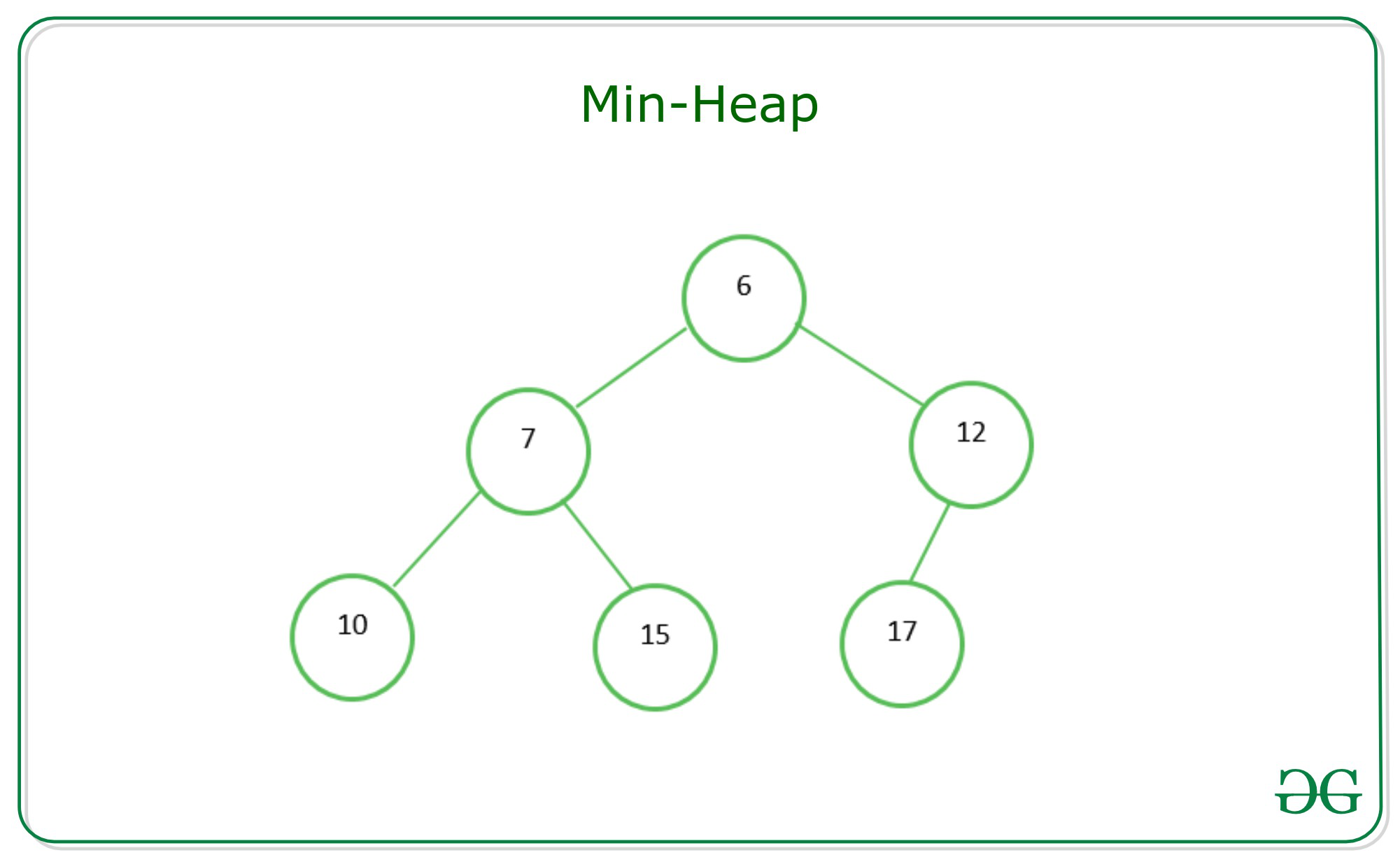
source: https://www.geeksforgeeks.org/difference-between-min-heap-and-max-heap/
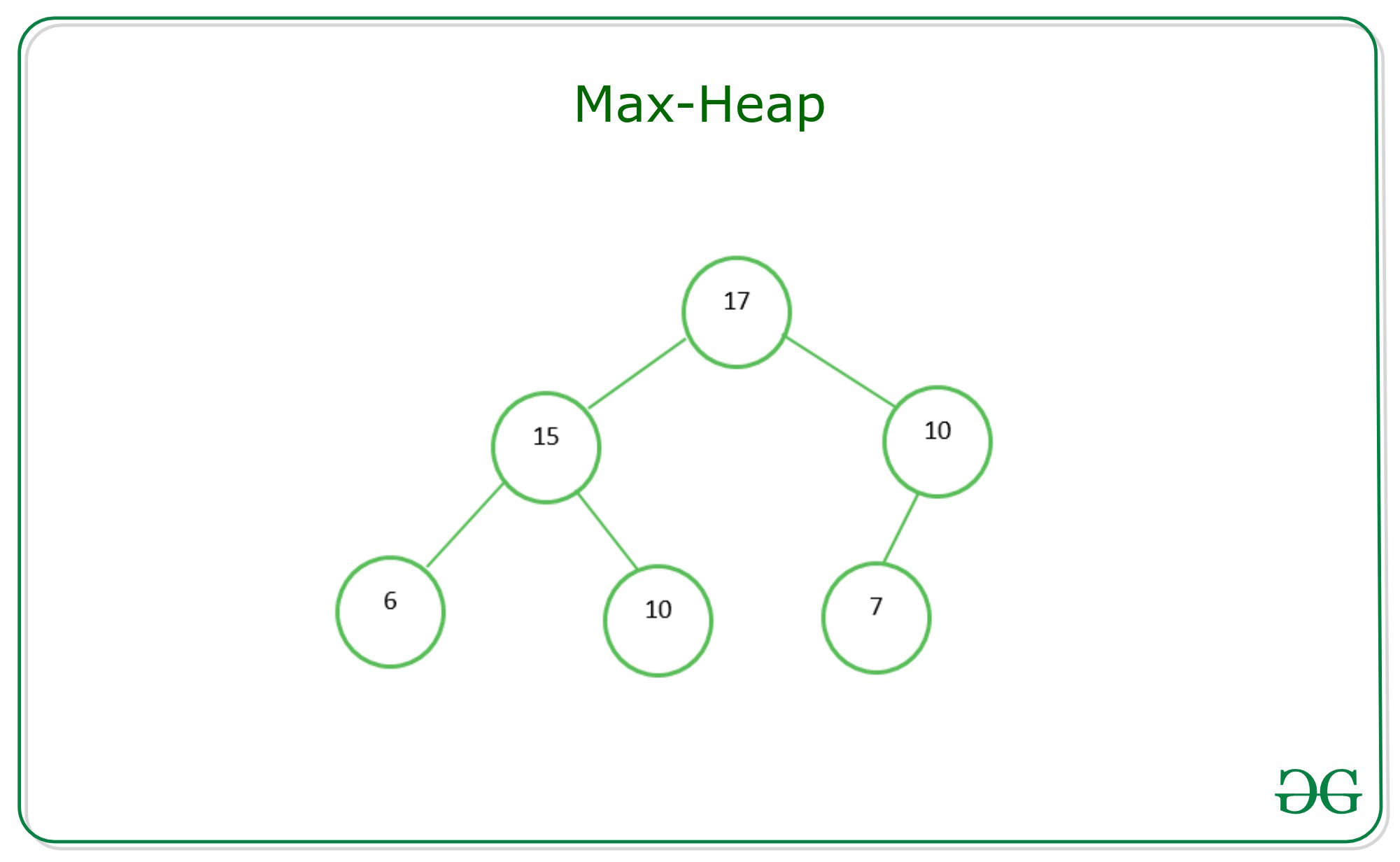
source : https://www.geeksforgeeks.org/difference-between-min-heap-and-max-heap/
📌 힙과 이진 탐색 드리의 공통점과 차이점
- 공통점 : “이진 트리”
- 차이점
2-1. 힙은 이진 탐색 트리의 조건인 자식노드 중 왼쪽과 오른쪽에 대한 구분이 없음
- 힙 : 각 노드의 값 ≥ 자식 노드의 값 or 각 노드의 값 ≤ 자식 노드의 값
- 이진 탐색 트리 : 해당 노드의 값 > 해당 노드의 왼쪽 자식 노드의 값 && 해당노드의 값 < 해당노드의 오른쪽 자식 노드의 값
2-2. 힙은 최대/최소값 탐색을 위한 구조 vs 이진 탐색 트리는 탐색을 위한 구조
🌟 힙에 데이터 삽입하기 - 기본 동작
- 왼쪽 최하단부 노드부터 채워지는 형태로 삽입
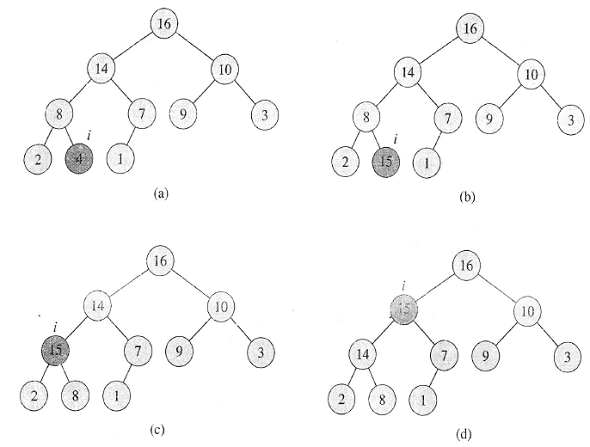
위의 그림처럼 Max Heap의 경우를 생각해보자
이 때, 삽입될 데이터가 존재하게 될 위치를 기준으로, 부모노드의 값보다 큰 값이 존재한다면, 부모노드와 swap 해주어야 한다!(루트노드까지 고려!)
🌟 힙의 데이터 삭제하기 - 기본 동작
마찬가지로 Max Heap에서 힙의 데이터를 삭제해보는 것을 생각해보자
-
보통 삭제는 루트노드를 삭제하는 것이 일반적!(최댓값과 최솟값을 바로 꺼내쓸 수 있도록 하는 것이 목적이기 때문과 관련)
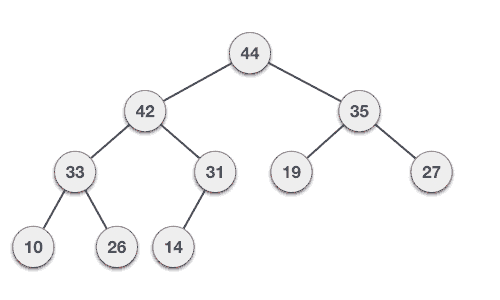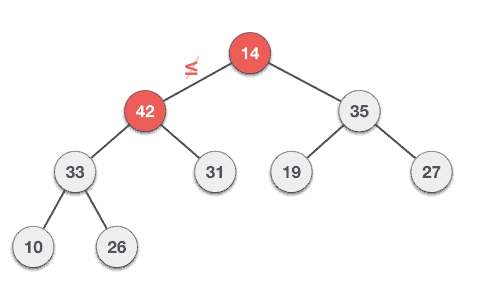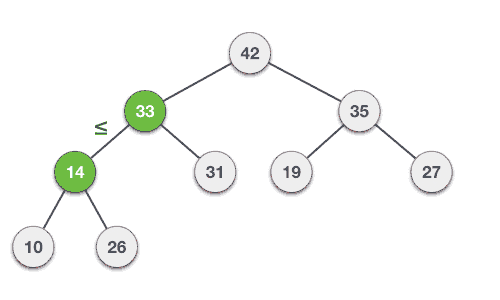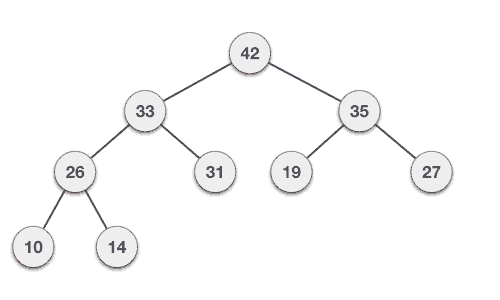
source: https://www.tutorialspoint.com/data_structures_algorithms/heap_data_structure.htm
- 루트노드 삭제
- 최하단 depth 노드들 중 왼쪽에서 가장 먼 노드(최근에 들어온 노드)를 루트노드로 이동
- 부모노드와 자식노드를 비교해서 부모노드값 ≤ 자식노드의 값인 경우 해당 노드들 간 swap
- 3의 과정 반복
최대 힙을 한번 구현해보자!
- 일반적으로 힙 구현시에는 배열 자료구조를 활용 -배열의 길이가 정해져 있는 것은 아니므로 ArrayList를 사용
- 배열은 인덱스 0 부터 시작하지만, 구현의 편의를 위해서 root 노드 인덱스를 1로 지정하면 구현이 보다 수월
- 부모 노드 인덱스 번호 = 자식 노드 인덱스번호/2
- 왼쪽 자식 노드 인덱스 번호 = 부모 노드 인덱스 번호 * 2 -오른쪽 자식 노드 인덱스 번호 = 부모 노드 인덱스 번호 * 2+1
그러면, 0번 인덱스는 비우고, 1번 인덱스부터 채워지므로, 생성자까지만 작성해본다면 아래와 같이 채워줄 수 있을 것이다!
package com.dataStructure.heap;
import java.util.ArrayList;
public class MaxHeap {
private ArrayList<Integer> heapArr = null;
public ArrayList<Integer> getHeap(){
return heapArr;
}
//복잡도를 낮추기 위해서 위에서의 제네릭스에 사용된 래퍼 클래스를 사용
public MaxHeap(Integer data){
heapArr = new ArrayList<>();
//0번 인덱스는 비워둘것(null)
**heapArr.add(null);**
//1번 인덱스에 루트노드
heapArr.add(data);
}
}
그러면 루트노드가 잘 삽입되었는지 확인해보자
package com.dataStructure.heap;
public class HeapTest {
public static void main(String[] args){
MaxHeap maxHeap = new MaxHeap(3);
System.out.println(maxHeap.getHeap());//[null, 3]
}
}
그러면 콘솔에 “[null, 3]”이 출력되어 인덱스 1에 루트노드가 등록된 것을 확인해볼 수 있다!
이번에는 노드를 삽입해보자
📌 Collections.swap(List list, int a, int b) 메서드
- list: 스왑할 데이터들이 들어있는 배열 변수
- a, b : 스왑할 데이터 인덱스 번호
위에서 공부한 내용을 상기해보면
- 일반적으로 힙 구현시에는 배열 자료구조를 활용 -배열의 길이가 정해져 있는 것은 아니므로 ArrayList를 사용
- 배열은 인덱스 0 부터 시작하지만, 구현의 편의를 위해서 root 노드 인덱스를 1로 지정하면 구현이 보다 수월
- 부모 노드 인덱스 번호 = 자식 노드 인덱스번호/2
- 왼쪽 자식 노드 인덱스 번호 = 부모 노드 인덱스 번호 * 2 -오른쪽 자식 노드 인덱스 번호 = 부모 노드 인덱스 번호 * 2+1
의 규칙이 있다! 이를 적용해보면
먼저, 의미상으로 걸러낼 코너케이스는 (물론 생성자에서 걸러냈지만)”힙이 비워져 있는 경우”인데, 이때에는 생성자에서 진행된 바와 동일하게 진행하면 될 것이다!
그런데, 그렇지 않고 한 개 이상의 노드가 있다면?
- 우선 arraylist는 왼쪽부터 차곡차곡 쌓이므로 먼저 넣어보고
- 지금 넣은 위치를 size()를 이용해보면 쉽게 알 수 있다!
- 그리고 부모노드와 비교가 필요하므로 2로 나눈 몫을 저장해주자
- 그리고 최대힙의 조건을 만족할 때까지(단, 부모노드와 자식노드의 값이 null인 경우를 배제하도록 명시해주자) swap해주고, 이에 따른 두 노드의 인덱스 값도 갱신해주자
//insert
public boolean insert(Integer data){
if(heapArr==null){
//데이터가 비워져 있는 경우(생성자에서 이미 생성되었겠지만 의미상 생각)
heapArr = new ArrayList<>();
heapArr.add(null);
heapArr.add(data);
}else{
int curIdx = 0;
int parentIdx =0;
heapArr.add(data);
curIdx = heapArr.size()-1;//최근에 삽입했으므로
//부모노드 인덱스=자식노드인덱스/2
parentIdx=curIdx/2;
//부모노드와 비교 후 swap
//heapArr.get(parentIdx)>=heapArr.get(curIdx)가 될때까지!
while(heapArr.get(parentIdx)!=null&& heapArr.get(curIdx)!=null&&heapArr.get(parentIdx)<heapArr.get(curIdx)){
Collections.swap(heapArr,parentIdx,curIdx);
curIdx = parentIdx;//부모노드와 swap되었으므로 부모노드 인덱스 값으로 바꿔주기
parentIdx=curIdx/2;//바꿔진 위치로 인해 부모노드도 새로이 세팅
}
}
return true;
}
package com.dataStructure.heap;
public class HeapTest {
public static void main(String[] args){
MaxHeap maxHeap = new MaxHeap(3);
System.out.println(maxHeap.getHeap());//[null, 3]
maxHeap.insert(5);
maxHeap.insert(6);
maxHeap.insert(7);
maxHeap.insert(8);
System.out.println(maxHeap.getHeap());
}
}
그러면 이전에 swap하지 않았을 때에는 “[null, 3, 5, 6, 7, 8]”의 값이 콘솔에서 확인되었지만 지금은 최대힙의 모양인 “[null, 8, 7, 5, 3, 6]”이 출력되는 것을 확인해볼 수 있다!
그리고 삭제도 상세히 나눠보면
- 힙에 데이터가 없으면 false로 할수 없음을 알리고
- 아니라면 루트노드를 삭제하고, 가장 마지막에 들어온 노드를 루트노드로 바꿔주는데
이는 루트노드와 마지막 노드를 바꿔주고, 마지막 노드 위치를 삭제하는 것과 같다!
- 그리고 최대힙 구조로 구조화해준다
의 규칙이 있다!
그런데, swap을 하기 위한 조건도 케이스를 나눠보면
case 1. 부모노드의 자식이 없는 경우-스왑대상이 아님
case 2. 부모노드의 왼쪽 자식만 있는 경우- 최대힙 구조에 부적절하면 스왑대상으로 판단
case 3. 부모노드의 모든 자식이 다 있는 경우- 최대힙 구조에 부적절하면 스왑대상으로 판단
와 같이 생각해볼 수 있는데, 완전 이진 트리이기 때문에 오른쪽 자식만 있는 경우는 존재할 수가 없다!
이를 while루프에서 조건에 따른 반복을 해주기 위해서 따로 메서드를 빼내어 진행해보면
아래와 같이 생각해볼 수 있다!
//delete 조건 체크-자식노드와 변경해야할 지 확인
public boolean canImoveDown(Integer parentIdx){
Integer rChild;
Integer lChild;
lChild=2*parentIdx;
rChild=lChild+1;
//case1: 왼쪽 자식 노드도 없을 때(왼쪽자식이 없으면 오른쪽자식도 없기 때문)
//<=>자식 노드가 없을 때
if(lChild >=heapArr.size()){//현재 배열 크기보다 계산한 값이 더 크다는 것은 계산한 값만큼
//데이터가 들어가지 않았다는 뜻
//즉 그만큼 데이터가 들어가지 않았다는 뜻
return false;//swap을 할 수 없음
//case2 : 오른쪽 자식노드만 없을 때-swap 가능
}else if(rChild>=heapArr.size()){
if(heapArr.get(parentIdx)< heapArr.get(lChild)){
return true;
}else{
return false;
}
//case3 : 왼쪽 자식노드와 오른쪽 자식 노드 모두 있을 때-swap 가능
}else{
if(heapArr.get(lChild)>heapArr.get(rChild)){
//왼쪽이 더 큰 경우
if(heapArr.get(parentIdx) < heapArr.get(lChild)){
return true;
}else{
return false;
}
}else{
//오른쪽이 더 큰 경우
if(heapArr.get(parentIdx) < heapArr.get(rChild)){
return true;
}else{
return false;
}
}
}
}
//delete
public Integer delete(){
//힙에 데이터가 없는 경우
if(heapArr==null){
return null;
}else{
//delete를 통해 가져갈 값
Integer returnedData;
//비교해야할 노드의 인덱스 번호
Integer parentIdx;
//parentIdx를 기준으로 존재하는 왼쪽과 오른쪽 노드
Integer lChild;
Integer rChild;
returnedData=heapArr.get(1);
//루트노드 삭제 && 마지막 노드가 루트노드로 갱신됨
heapArr.set(1,heapArr.get(heapArr.size()-1));
heapArr.remove(heapArr.size()-1);
parentIdx=1;
//힙 구조에 맞춰주기
while(canImoveDown(parentIdx)){
lChild=2*parentIdx;
rChild=lChild+1;
//return true만 케이스별 처리
//case 2: 오른쪽 자식 노드만 없을때
if(rChild>=heapArr.size()){
//왼쪽은 있는 상황
if(heapArr.get(parentIdx)<heapArr.get(lChild)){
//swap
Collections.swap(heapArr,parentIdx,lChild);
}
}else{
//case 3: 왼쪽과 오른쪽 자식노드 모두 있을 때
//case 3-1: 왼쪽이 더 큰 경우
if(heapArr.get(lChild)>heapArr.get(rChild)){
//왼쪽과 부모노드 비교
if(heapArr.get(lChild)>heapArr.get(parentIdx)){
Collections.swap(heapArr,parentIdx,lChild);
}
}else{
//오른쪽이 더 큰 경우
//오른쪽과 부모노드 비교
if(heapArr.get(rChild)>heapArr.get(parentIdx)){
Collections.swap(heapArr,parentIdx,rChild);
}
}
}
}
return returnedData;
}
}
위와 같다!
이를 테스트해보면
package com.dataStructure.heap;
public class HeapTest {
public static void main(String[] args){
MaxHeap maxHeap = new MaxHeap(3);
System.out.println(maxHeap.getHeap());//[null, 3]
maxHeap.insert(5);
maxHeap.insert(6);
maxHeap.insert(7);
maxHeap.insert(8);
System.out.println(maxHeap.getHeap());//[null, 3, 5, 6, 7, 8]->[null, 8, 7, 5, 3, 6]
maxHeap.delete();
System.out.println(maxHeap.getHeap());
}
}
“[null, 7, 6, 5, 3]”이 출력된다!
즉, 삭제도 잘 반영되었음을 확인해볼 수 있다!