1_[datastructure]트리구조

7 minute read

트리

노드와 가지(branch)를 이용해서 사이클을 이루지 않도록 구성한 데이터 구조
이진 트리 형태 구조를 기반으로 한 탐색(검색) 알고리즘 구현에 많이 사용됨

📌 알아둘 용어 📌

노드 : 트리에서 데이터를 저장하는 기본 요소
- 데이터
- 다른 연결된 노드에 대한 브랜치 정보
루트노드 : 트리의 맨 위에 있는 노드
레벨 : 최상위 노드를 Level 0으로 하였을 때, 하위 브랜치로 연결된 노드의 깊이
부모노드 : 어떤 노드의 상위 레벨에 연결된 노드
자식노드 : 어떤 노드의 다음 레벨에 연결된 노드
리프 노드(단말 노드; Terminal Node) : 자식 노드가 하나도 없는 노드
형제(자매)노드 : 동일한 부모 노드를 가진 노드
깊이 : 트리에서 노드가 가질 수 있는 최대 레벨(위의 그림에서 Depth 깊이는 3)

🌟 이진 트리와 이진 탐색 트리(Binary Search Tree) 🌟

이진 트리 : 노드의 최대 브랜치가 2인 트리
이진 탐색 트리 (Binary Search Tree; BST) : 이진트리에 다음과 같은 추가적인 조건이 있는 트리
왼쪽 노드 < 해당 노드
해당 노드 < 오른쪽 노드

source: https://blog.penjee.com/5-gifs-to-understand-binary-search-tree/#binary-search-tree-insertion-node

🌻 이진 탐색 트리의 장점 및 주요 용도

주요 용도 : 데이터 검색(탐색)
장점 : 탐색 속도를 개선할 수 있음

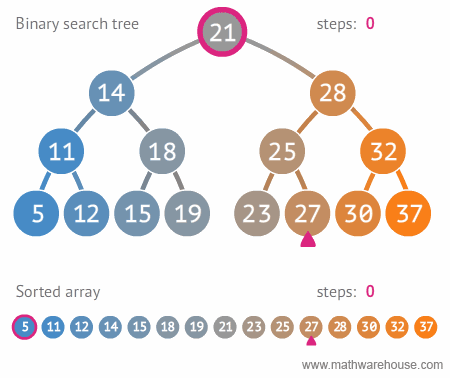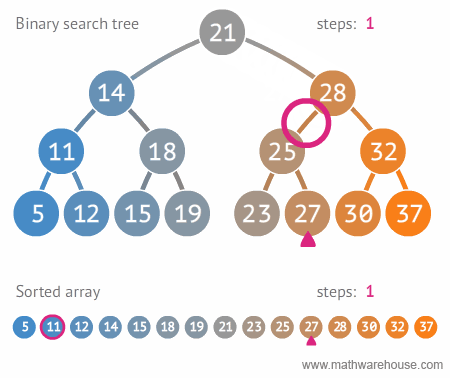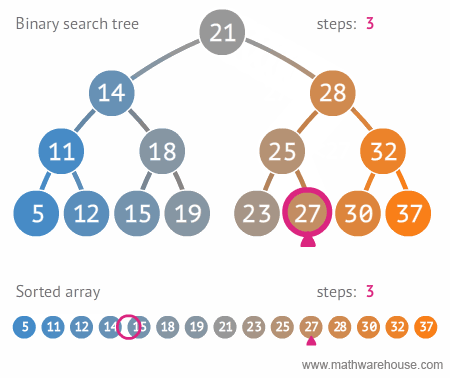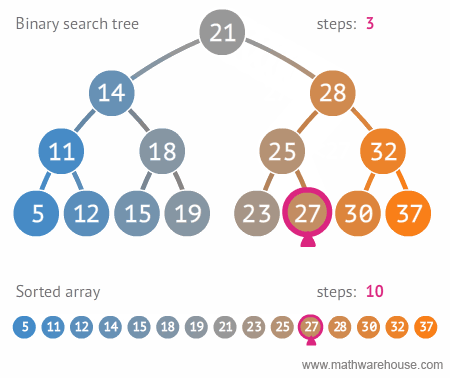
source: https://blog.penjee.com/5-gifs-to-understand-binary-search-tree/#binary-search-tree-insertion-node

먼저 트리를 위한 노드를 관리하는 클래스 NodeMgmt를 만들어보자

package com.dataStructure.tree;
//노드를 관리할 수 있는 클래스
public class NodeMgmt {
    //노드
   . public class Node{
        //왼쪽 브랜치
        Node left;
        //오른쪽 브랜치
        Node right;
        //data
        int value;

        //constructor
        public Node(int data){
            this.value=data;
            this.left=null;
            this.right=null;
        }
    }
}

먼저 노드를 내부 클래스로 관리하게 하는데 브랜치가 왼쪽과 오른족으로 존재할 것이고, 데이터가 있을 것이기 때문에 필드는

Node left
Node right
int value

가 될 수 있다!

그리고 노드를 관리하는 필드는 루트노드가 필요하기 때문에 루트노드를 필드로 가져야 한다! 그런데 현재는 루트노드에 연결되어 있는지는 추후 과정에서 고려될 부분이기에, null로 초기화해주자

package com.dataStructure.tree;
//노드를 관리할 수 있는 클래스
public class NodeMgmt {
    //노드
    public class Node{
        //왼쪽 브랜치
        Node left;
        //오른쪽 브랜치
        Node right;
        //data
        int value;

        //constructor
        public Node(int data){
            this.value=data;
            this.left=null;
            this.right=null;
        }
    }
    Node root=null;
}

이번에는 노드를 삽입하는 것을 생각해보자

노드를 삽입해야 될 경우에는 아래와 같은 일련의 규칙을 기반으로 진행될 것이다

루트노드부터 탐색을 시작한다 2.. 현재노드보다 왼쪽으로 삽입되어야 할 경우
- 왼쪽노드가 존재하면, 그 존재하는 왼쪽노드를 기준으로 재탐색
- 왼쪽노드가 비어있다면, 그 위치에 새 노드를 생성 후 루프 탈출
현재노드보다 오른쪽으로 삽입되어야 할 경우
- 오른쪽 노드가 존재하면, 그 존재하는 오른쪽 노드를 기준으로 재탐색 - 오른쪽 노드가 비어있다면, 그 위치에 새 노드를 생성 후 루프 탈출

//데이터 삽입
    public boolean insertNode(int data){
        //case 1: 노드가 하나도 없을 때
        if(root==null){
            this.root=new Node(data);
        }else{
            //case 2:노드가 하나 이상 들어가 있을 때
            //정확한 노드의 위치를 찾은 다음에 데이터를 넣어주어야 함
            Node finder = this.root;

            while(true){
                //case2-1. 현재 노드의 왼쪽에 노드가 들어가야 할 때
                if(**data < finder.value**){
                    //왼쪽에 있는 노드가 있는지 확인
                    if(finder.left!=null){
                        //존재하고 있었다면 왼쪽으로 옮겨서
                        //탐색을 이어가야할 것
                        finder=finder.left;
                    }else{
                        finder.left=new Node(data);
                        break;//clear되었기 때문에 더이상 반복하지 않아도 됨
                    }
                }else{
                    //case2-2 . 현재 노드의 오른쪽에 노드가 들어가야 할 때
                    if(finder.right!=null){
                        finder=finder.right;
                    }else{
                        finder.right=new Node(data);
                        break;
                    }
                }
            }
        }
        return true;
    }

그리고 노드가 생성될 때 left와 right가 null로 생성되었는데 위의 메서드의 분기문을 통해서 이 부분이 해소될 수 있음을 생각해볼 수 있다(루트노드도 마찬가지)

이번에는 이진 트리 탐색을 진행해보자

탐색은 아래의 규칙을 기반으로 진행된다

트리가 비어있다면 null을 반환
트리 내부 노드가 1개 이상이라면 루트노드부터 시작해서 해당 노드를 탐색 2-1.해당 노드를 찾은 경우 그 노드를 반환 2-2.해당노드를 찾지 못한 경우-탐색 진행 2-2-1.과정을 진행하는 노드의 값 > 인자로 주어진 값[=탐색 대상] ▶️ 왼쪽 탐색 2-2-2.과정을 진행하는 노드의 값 < 인자로 주어진 값[=탐색 대상] ▶️ 오른쪽 탐색
2-1과 2-2의 과정을 거치고도 못찾은 경우는 없는 것이므로 null을 반환

위의 규칙을 기반으로 한다면, 아래와 같이 탐색에 대해서 생각해볼 수 있다

//이진 트리 탐색
    //데이터를 가진 노드를 발견하면 노드를 반환
    public Node search(int data){
        //case 1 : 노드가 하나도 없을 때
        if(this.root==null){
            return null;
        }else{
            //case 2 : 노드가 하나 이상 있을 때
            //루트노드부터 시작해서 해당 노드를 찾기
            Node finder = this.root;

            while(finder!=null){
                if(finder.value==data){
                    //case 2-1. 해당 노드를 찾은 경우
                    return finder;
                }else{
                    //case 2-2. 해당 노드를 찾지 못한 경우
                    //case 2-2-1. data<finder.value
                    if(data<finder.value){
                        //왼쪽으로 탐색
                        finder=finder.left;
                    }else{
                        //case 2-2-2. data>finder.value
                        //오른쪽으로 탐색
                        finder=finder.right;
                    }

                }
            }
            //못찾은 경우
            return null;
        }

간단하게 Node클래스에서 toString을 오버라이딩해주고 테스트해보자

package com.dataStructure.tree;

public class TreeMain {
    public static void main(String[] args){
        NodeMgmt tree = new NodeMgmt();

        tree.insertNode(2);
        tree.insertNode(3);
        tree.insertNode(4);
        tree.insertNode(5);
        tree.insertNode(6);

        NodeMgmt.Node test = tree.search(3);
        System.out.println(test);
        System.out.println(test.value);//3
        System.out.println("===");
        System.out.println(tree.search(0));//null
    }
}

그러면 노드가 탐색되면 루트노드부터 차례대로 출력되고, value 값도 확인해볼 수 있다

하지만 존재하지 않은 경우 null이 출력됨을 확인해볼 수 있다

그리고 지금은 2가 루트노드이고, 2보다 작은 값이 없어서 left 속성은 null일 것이다

package com.dataStructure.tree;

public class TreeMain {
    public static void main(String[] args){
        NodeMgmt tree = new NodeMgmt();

        tree.insertNode(2);
        tree.insertNode(3);
        tree.insertNode(4);
        tree.insertNode(5);
        tree.insertNode(6);

        NodeMgmt.Node test = tree.search(3);
        System.out.println(test);
        System.out.println(test.value);//3
        System.out.println("===");
        System.out.println(tree.search(0));//null
        System.out.println("===");
        System.out.println(test.right.value);//4
        System.out.println("===");
        System.out.println(test.left);//null
    }
}

이를 위의

test.right.value test.left

를 출력하는 부분에서 확인해볼 수 있다

하지만 이를

				tree.insertNode(0);
        test=tree.search(2);
        System.out.println(test.left.value);

루트노드인 2보다 작은 0을 값으로 넣어주고

탐색설정을 다시 설정해주면 콘솔에 test.left.value의 값이 “0”이라고 표시되는 것을 확인해볼 수 있다

이번에는 이진 탐색 트리(BST)에서 특정 노드를 삭제해보자

삭제할 노드가 리프노드인 경우
- 리프노드의 부모노드에서 리프노드와 연결되는 브랜치 연결을 해제시키기

자식 노드가 1개인 노드를 삭제
- 삭제할 노드의 부모노드와 자식노드를 연결해주어야!

🌟자식 노드가 두 개인 노드 삭제

방법은 2가지가 있는데 “방법1”로 공부해볼 것!

방법 1. 삭제할 노드의 오른쪽 자식 중 가장 작은 값을 삭제할 노드의 부모노드가 가리키도록 하기

방법 2. 삭제할 노드의 왼쪽 자식 중 가장 큰 값을 삭제할 노드의 부모노드가 가리키도록 하기

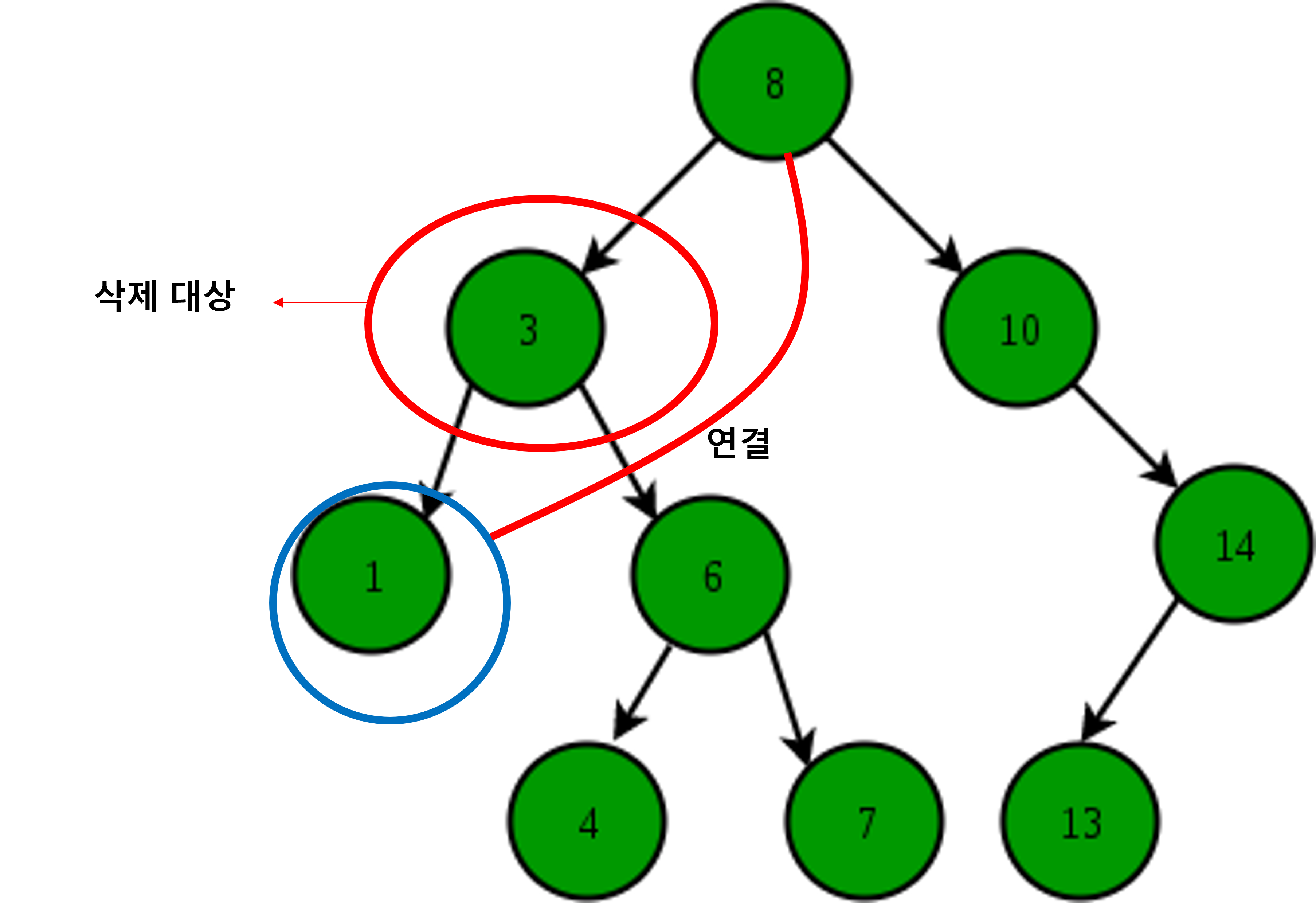
위의 두 방법의 공통점은 지금 “3”이라고 적혀진 노드의 위치로 옮겨지게 되면, 이진 검색 트리의 기준에 아주 잘 맞게 된다는 점이다!(왼쪽의 값이 더 작고, 오른쪽 값이 더 크다는 기준!)

그래서 방법 1의 과정을 정리해보면

삭제할 노드의 오른쪽 자식 노드 선택
오른쪽 자식의 가장 왼쪽에 있는 노드를 선택
해당 노드를 삭제할 노드의 부모노드의 왼쪽 브랜치가 가리키도록 함
해당 노드의 왼쪽 브랜치가 “해당 노드의 삭제할 노드의 부모노드의 왼쪽 자식노드”를 가리키도록 함 5.해당노드의 오른쪽 브랜치가 삭제할 노드의 오른쪽 자식 노드를 가리키도록 함

위와 같다!

위의 3 가지 케이스를 조합하여 삭제를 진행해보면 아래와 같다!

//이진 탐색 트리 삭제
    //삭제할 노드 탐색
    public boolean delete(int value){
        boolean searched =false;

        Node currParent= this.root;//루트노드부터 탐색
        Node curr = this.root;

        //코너 케이스1. 노드가 하나도 없을 때
        if(this.root==null){
            return false;
        }else {
            //코너 케이스 2: 노드가 단지 하나만 있고, 해당 노드가 삭제할 노드일 때
            if(this.root.value==value && this.root.left==null && this.root.right==null){
                this.root=null;
                return true;
            }
        //아닌 경우 순회
            while(curr!=null){
                if(curr.value==value){
                    searched=true;
                    break;
                }else if(value<curr.value){
                    currParent=curr;//부모노드 위치를 업데이트하면서
                    //왼쪽 순회
                    curr=curr.left;
                }else if(value>curr.value){
                    currParent=curr;
                    //오른쪽 순회
                    curr=curr.right;
                }
            }
            //while루프를 끝나고 나서 탐색이 끝난 경우도 있을 것이고
            //못찾은 경우도 있을 것
            if(searched==false){
                //찾지못한 경우는 바로 false 리턴
                return false;
            }
        }
        //여기까지 실행되면
        //curr: 삭제 대상 데이터를 갖고 있는 노드
        //currParent: 삭제 대상 데이터를 갖고 있는 노드의 부모노드

        //case1 : 삭제할 노드가 리프노드인 경우
        if(curr.left==null && curr.right==null){
            if(value<currParent.value){
                //지금 value를 갖고 있는 노드가
                //curr인데 이 값이 부모노드보다 작다는 것은
                //해당 노드가 부모노드의 왼쪽 브랜치와 연결되어 있었다는 것!
                //따라서 왼쪽 브랜치를 비워주기
                currParent.left=null;
                curr=null;//명시적으로 가독성을 높이기 위함
            }else{
                //부모노드의 오른쪽에 있었던것
                currParent.right=null;
                curr=null;
            }

            return true;
        }else if(curr.left!=null && curr.right==null){
            //case 2-1: 삭제할 노드가 자식노드를 한 개 갖고 있는 경우(왼쪽)
            if(value < currParent.value){
                //해당 노드는 부모노드의 왼쪽에 존재했던 것
                currParent.left=curr.left;//해당노드의 왼쪽 노드와 부모노드의 왼쪽 브랜치를 연결
                //명시적으로 작성
                curr=null;
            }else{
                //해당노드는 부모노드의 오른쪽에 존재했던 것
                //부모노드의 오른쪽과 현재노드의 왼쪽을 연결(현재노드의 왼쪽만 존재하기 때문)
                currParent.right=curr.left;
                curr = null;
            }
            return true;
        }else if(curr.left==null && curr.right!=null){
            //case 2-2: 삭제할 노드가 자식노드를 한 개 갖고 있는 경우(오른쪽)
            if(value< currParent.value){
                //부모노드의 왼쪽과 현재노드의 오른쪽을 연결
                currParent.left=curr.right;
                curr=null;
            }else{
                //부모노드의 오른쪽과 현재노드의 오른쪽을 연결
                currParent.right=curr.right;
                curr=null;
            }
            return true;
        }else{
            //case 3-1.자식노드가 2개인 노드를 삭제(삭제할 노드가 왼쪽에 있을 때)
            //이 때, 가장 작은 값을 가진 노드는 , 오른쪽 브랜치를 갖거나 어떤 자식도 없거나!를 의미!
            if(value < currParent.value){
                Node changeNode = curr.right;//오른쪽 자식 중 가장 작은 값을 찾기 위함
                Node changeParentNode = curr.right;

                while(changeNode.left!=null){
                    changeParentNode=changeNode;
                    changeNode=changeNode.left;//작은 값 찾기
                }
                
                //changeNode: 삭제할 노드의 오른쪽 부분에서의 가장 작은 노드가 저장됨
                //case 3-1-1 changeNode의 자식노드가 없을 때
                if(changeNode.left==null && changeNode.right==null) {
                    changeParentNode.left=null;
                }else if(changeNode.right!=null){
                    //case 3-1-2 changeNode의 오른쪽 자식노드가 있을 때
                    changeParentNode.left=changeNode.right;//오른쪽 자식노드와 부모의 왼쪽 요소 연결
                }
                //currParentNode의 왼쪽 자식에 삭제할 노드의
                //오른쪽 자식 중 가장 작은 값을 가진 changeNode 연결
                currParent.left=changeNode;
                //원래 삭제될 노드의 자식노드와 연결
                changeNode.left=curr.left;
                changeNode.right=curr.right;

                curr=null;
            }else{
                //case 3-2.자식노드가 2개인 노드를 삭제(삭제할 노드가 오른쪽에 있을 때)
                Node changeNode = curr.right;//오른쪽 자식 중 가장 작은 값을 찾기 위함
                Node changeParentNode = curr.right;

                while(changeNode.left!=null){
                    changeParentNode=changeNode;
                    changeNode=changeNode.left;//작은 값 찾기
                }
                //changeNode: 삭제할 노드의 오른쪽 부분에서의 가장 작은 노드가 저장됨
                //case 3-2-1 changeNode의 자식노드가 없을 때
                if(changeNode.left==null && changeNode.right==null) {
                    changeParentNode.left=null;
                }else if(changeNode.right!=null){
                    //case 3-2-2 changeNode의 오른쪽 자식노드가 있을 때
                    changeParentNode.left=changeNode.right;//오른쪽 자식노드와 부모의 왼쪽 요소 연결
                }
                //currParentNode의 오른쪽 자식에 삭제할 노드의
                //오른쪽 자식 중 가장 작은 값을 가진 changeNode 연결
                currParent.right=changeNode;//부모의 오른쪽과 연결
                //원래 삭제될 노드의 자식노드와 연결
                changeNode.left=curr.left;
                changeNode.right=curr.right;

                curr=null;
            }
            return true;

        }

그리고 이를 테스트해보면 연결해제가 되어 삭제까지 잘 완료됨을 확인해볼 수 있다!

package com.dataStructure.tree;

public class TreeMain {
    public static void main(String[] args){
        NodeMgmt tree = new NodeMgmt();

        tree.insertNode(2);
        tree.insertNode(3);
        tree.insertNode(4);
        tree.insertNode(5);
        tree.insertNode(6);

        NodeMgmt.Node test = tree.search(3);
        System.out.println(test);
        System.out.println(test.value);//3
        System.out.println("===");
        System.out.println(tree.search(0));//null
        System.out.println("===");
        System.out.println(test.right.value);//4
        System.out.println("===");
  //      System.out.println(test.left);//null

        tree.insertNode(0);
        test=tree.search(2);
        System.out.println(test.left.value);

        tree.insertNode(1);
        tree.insertNode(10);
        tree.insertNode(11);
        tree.insertNode(12);
        tree.insertNode(13);

        tree.delete(13);
        test=tree.search(13);
        System.out.println(test);//null

        tree.delete(0);
        test= tree.search(0);
        System.out.println(test);//null

        tree.delete(4);
        test=tree.search(4);
        System.out.println(test);//null
        test=tree.search(2);//루트를 기준으로 모두 출력
        System.out.println(test);
        /*
        * Node{left=Node{left=null, right=null, value=1}, right=Node{left=null, right=Node{left=null, right=Node{left=null, right=Node{left=null, right=Node{left=null, right=Node{left=null, right=null, value=12}, value=11}, value=10}, value=6}, value=5}, value=3}, value=2}
        *           2
        *       x     3
        *           5   6
        *         10 11 12 x
        * */
    }
}

🌟 트리가 n개의 노드를 가지면 depth(트리의 높이)=$log(2)n$ 에 가깝기 때문에 시간목잡도=O(logn)[참고로 , 빅오표기법에서 log의 밑은 10이 아닌 2!!

즉, logn은 50% 실행시간 단축을 의미할 수 있다!]

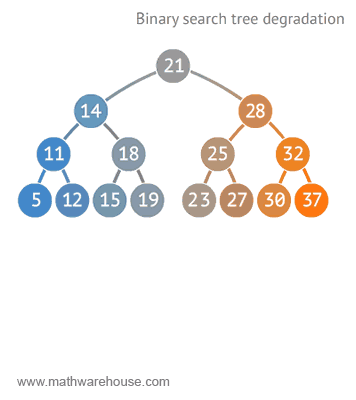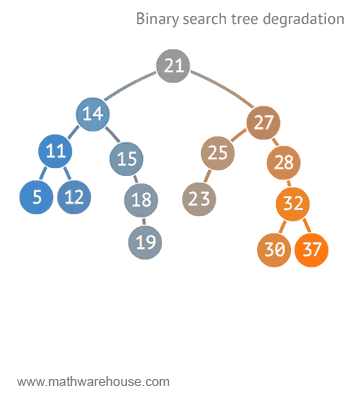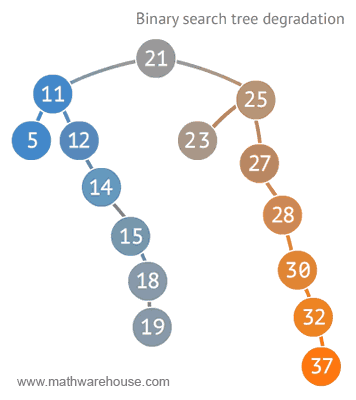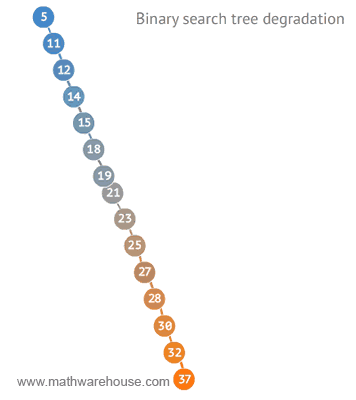
그런데 만약 이진 검색 트리가 아래처럼 단방향으로 일직선으로 구성된 경우 링크드리스트 등과 같이 동일 성능으로 O(n)을 보여주게 될 수도 있다![이진 검색 트리의 단점]

Twitter Facebook LinkedIn

J. S. Jeong

1_[datastructure]트리구조

트리

You May Also Enjoy

1_[spring]rest api 구축에 힘을 실어주는 hateoas

2_[spring jpa]m to n 연관관계 중간 테이블을 엔티티로 관리하는 경우

1_[spring jpa]m to n 연관관계 중간 테이블을 엔티티로 관리하지 않는 경우

2_[spring]websockethandler를 이용한 웹소켓 서버 구현